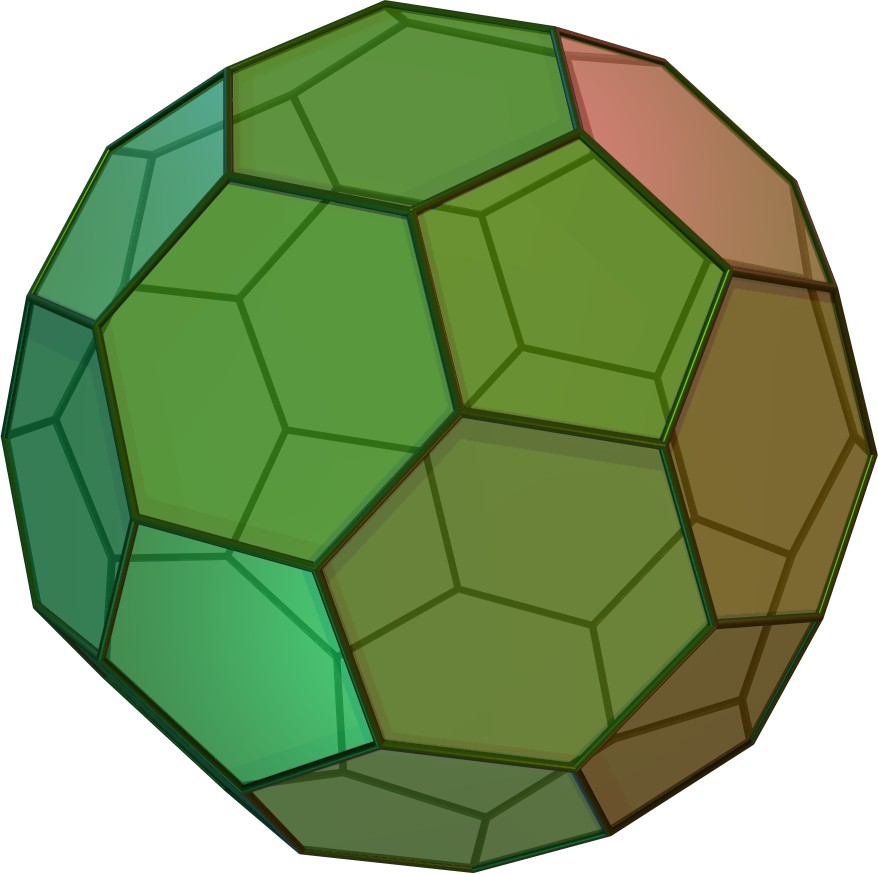
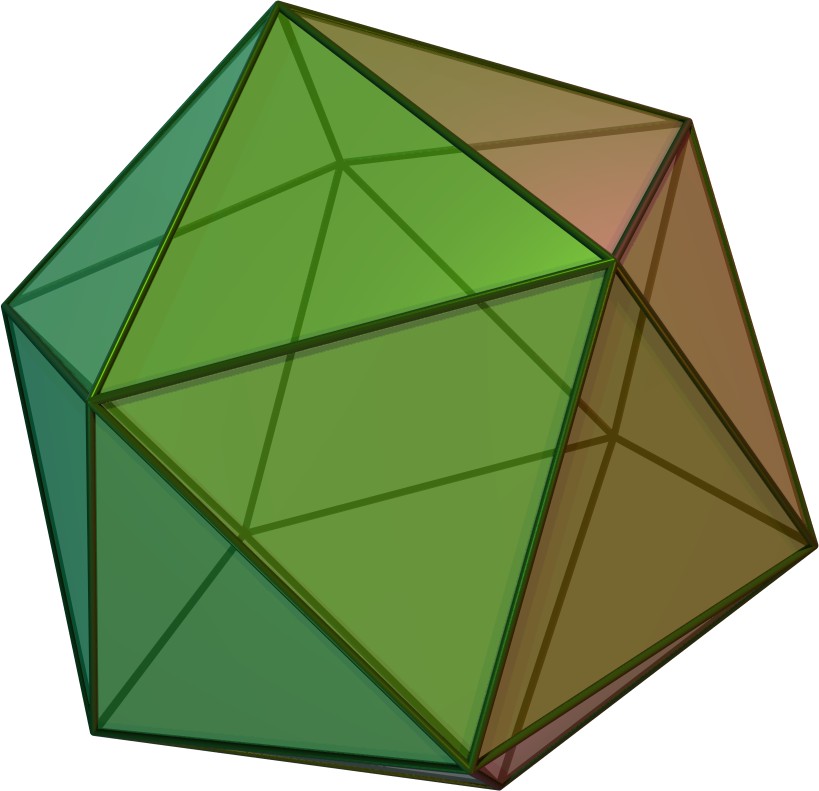
깎은 정십이면체

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 구성
- 2.1. 공식
3. 성질
4. 그래프
5. 관련 다면체
- 5.1. 비슷한 다면체
참조

1. 개요

깎은 정십이면체는 정십이면체의 꼭짓점을 깎거나 모서리를 확장하여 만들 수 있는 아르키메데스 다면체 중 하나이다. 32개의 면(정삼각형 20개, 정십각형 12개), 90개의 모서리, 60개의 꼭짓점을 가지며, 정이십면체 대칭을 갖는 준정다면체이다. 깎은 정십이면체는 겉넓이, 부피, 외접구 반지름을 계산하는 공식이 존재하며, 깎은 정십이면체 그래프는 60개의 꼭짓점과 90개의 변을 가진 정규 아르키메데스 그래프이다. 또한, 깎은 정십이면체는 증대 다면체 구성을 통해 다양한 존슨의 다면체를 생성하는 데 사용될 수 있다.

더 읽어볼만한 페이지

아르키메데스의 다면체 - 다듬은 정육면체
깎은 정육면체는 정육면체의 꼭짓점을 잘라 만든 다면체로, 6개의 정팔각형과 8개의 정삼각형으로 구성되고, 마름모 입방팔면체 등과 연관되며, 데카르트 좌표계와 트리보나치 수열로 꼭짓점 위치를 나타낼 수 있고, 키랄성 및 팔면체 대칭성을 가지며 여러 분야에 활용됩니다.
아르키메데스의 다면체 - 깎은 정이십면체
깎은 정이십면체는 정이십면체의 꼭짓점을 잘라낸 아르키메데스의 다면체로, 32개의 면, 90개의 변, 60개의 꼭짓점을 가지며, 축구공, 풀러렌 분자 등 다양한 분야에서 활용된다.

깎은 정십이면체
개요
깎은 정십이면체
종류	아르키메데스 다면체
대칭군	정이십면체 대칭 (I_h)
쌍대다면체	삼각 이십면체
면의 수	32
모서리의 수	90
꼭짓점의 수	60
꼭짓점 배열	10-10: 116.57° 3-10: 142.62°
꼭짓점 도형	Polyhedron truncated 12 vertfig.svg
전개도	Polyhedron truncated 12 net.svg
구성
면	정삼각형 20개, 정십각형 12개
꼭짓점	각 꼭짓점은 정삼각형 1개와 정십각형 2개로 구성됨 (3, 10²)
슐레플리 기호	t{5, 3}
위소프 기호	2 3 \| 5
속성	볼록 다면체

2. 구성

깎은 정십이면체는 정십이면체의 각 꼭짓점을 잘라내어 만들거나, 정십이면체의 모서리를 밀어내 오각형 면을 십각형 면으로, 꼭짓점을 삼각형으로 만들어 구성할 수 있다. 깎은 정십이면체는 32개의 면, 90개의 모서리, 60개의 꼭짓점을 가진다.

깎은 정십이면체는 데카르트 좌표계를 사용하여 구성할 수도 있다. 원점을 중심으로 하는 모서리 길이가 2φ − 2^영어일 때, 다음 좌표들의 짝수 순열 조합은 깎은 정십이면체의 꼭짓점 좌표가 된다.^[1]

(0, ±1/φ^영어, ±(2 + φ))
(±1/φ^영어, ±φ, ±2φ)
(±φ, ±2, ±(φ + 1))

여기서 φ = (1 + √5)/2^영어는 황금비이다.^[1]

2. 1. 공식

한 모서리의 길이가

a

인 깎은 정십이면체의 겉넓이

A

와 부피

V

, 외접구의 반지름은 다음과 같다.^[3]

:

A = 5\left(\sqrt{3}+6\sqrt{5+2\sqrt{5}}\right) a^2 \approx 100.991a^2

:

V = \frac{5}{12} \left(99+47\sqrt{5}\right) a^3 \approx 85.040a^3

:외접구 반지름:

\frac{\sqrt{74+30\sqrt{5}}}{4}a \approx 2.969449a

3. 성질

깎은 정십이면체는 아르키메데스 다면체 중 하나로, 매우 대칭적인 준정다면체이다. 정이십면체와 같은 정이십면체 대칭을 갖는다.^[6] 모든 꼭짓점에서는 정삼각형 1개와 정십각형 2개가 만나며, 깎은 정십이면체의 꼭짓점 도형은 $3 \cdot 10^2$ 이다. 깎은 정십이면체의 쌍대다면체는 삼각십이면체이며 카탈랑 다면체에 속하고, 깎은 정십이면체와 같은 대칭성을 갖는다.

깎은 정십이면체는 키랄성이 없어서 거울상과 합동이다.^[3]

깎은 정십이면체의 두 정십각형 면 사이의 이면각은 116.57°이고, 정삼각형과 정십각형 사이의 이면각은 142.62°이다.

변의 길이가

a

일 때 겉넓이

A

와 부피

V

는 다음과 같다.

:

\begin{align}A &= 5 \left(\sqrt{3}+6\sqrt{5+2\sqrt{5}}\right) a^2 &&\approx 100.991a^2 \\V &= \frac{5}{12} \left(99+47\sqrt{5}\right) a^3 &&\approx 85.040a^3\end{align}

4. 그래프

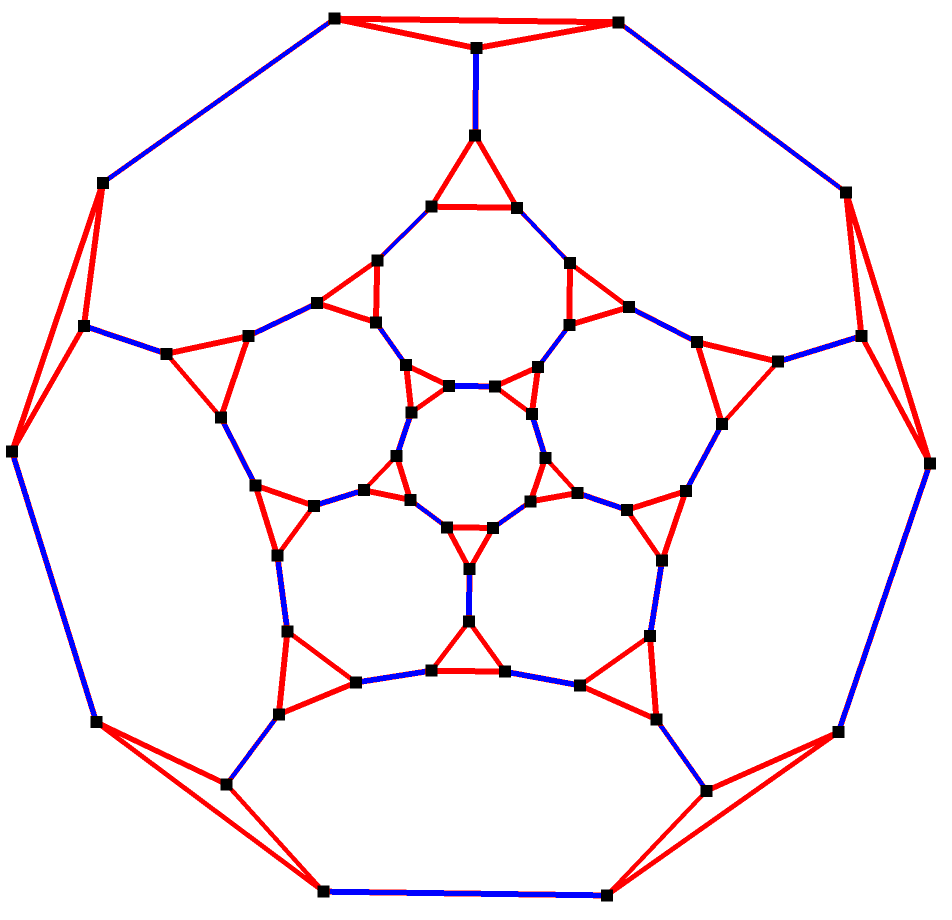
수학의 그래프 이론 분야에서, '''깎은 정십이면체 그래프'''는 아르키메데스 도형 중 하나인 '''깎은 정십이면체'''의 꼭짓점과 변으로 이루어진 그래프이다. 60개의 꼭짓점과 90개의 변을 가지며, 정규 아르키메데스 그래프이다.

5. 관련 다면체

깎은 정십이면체는 증대 다면체 구성에 적용될 수 있다. 예를 들어 깎은 정십이면체에 오각뿔을 부착하여 존슨의 다면체를 만들 수 있는데, 여기에는 증대 깎은 정십이면체, 이중 증대 깎은 정십이면체, 메타 이중 증대 깎은 정십이면체, 삼중 증대 깎은 정십이면체가 있다.^[1]

5. 1. 비슷한 다면체

--

참조

_[1] Mathworld Icosahedral group
_[2] 논문 Regular-faced convex polyhedra
_[3] 서적 Multi-shell Polyhedral Clusters https://books.google[...] Springer
_[4] 서적 Shapes, Space, and Symmetry https://books.google[...] Courier Corporation
_[5] 논문 Convex polyhedra with regular faces
_[6] 간행물 Mathematical Physics: Proceedings of the 13th Regional Conference, Antalya, Turkey, 27–31 October 2010 World Scientific
_[7] 서적 An Atlas of Graphs Oxford University Press
_[8] 서적 ICGG 2018 - Proceedings of the 18th International Conference on Geometry and Graphics: 40th Anniversary - Milan, Italy, August 3-7, 2018
_[9] 서적 The Geometrical Foundation of Natural Structure: A Source Book of Design https://archive.org/[...] Dover Publications, Inc.
_[10] 논문 Truncated Truncated Dodecahedron and Truncated Truncated Icosahedron Spaces

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com